Le Macchine di Turing

Antonio Brogi      Antonio Cisternino      Francesco Romani

Dipartimento di Informatica
Università di Pisa

Premessa 

Nonostante tutto questo, il comportamento delle macchine di Turing può essere spiegato in modo semplice a chi non possiede conoscenze di informatica. Abbiamo per questo deciso di preparare un'introduzione alla macchine di Turing che fosse breve ed al tempo stesso auto-contenuta. 

Che cosa è una macchina di Turing? 

Una macchina di Turing (MdT) è definita da un insieme di regole che definiscono il comportamento della macchina su un nastro di input-output (lettura e scrittura). Il nastro può essere immaginato come un nastro di carta di lunghezza infinita, diviso in quadratini dette celle. Ogni cella contiene un simbolo oppure è vuota. Una MdT ha una testina che si sposta lungo il nastro leggendo, scrivendo oppure cancellando simboli nelle celle del nastro. La macchina analizza il nastro, una cella alla volta, iniziando dalla cella che contiene il simbolo più a sinistra nel nastro. 

Ad ogni passo, la macchina legge un simbolo sul nastro e in accordo al suo stato interno corrente: 

1.decide il suo prossimo stato interno, e 

2.scrive un simbolo sul nastro e decide se spostare o meno la testina a sinistra o a destra di una posizione. 

Come per uno stato della mente di un essere umano, lo stato interno di una MdT definisce l'ambiente in cui una decisione viene presa. Una MdT può avere solo un numero finito di stati. 

Il comportamento di una MdT può essere programmato definendo un insieme di regole, o quintuple, del tipo: 

(stato-interno-corrente,  simbolo-letto,  prossimo-stato-interno,  simbolo-scritto,  direzione). 

Per esempio la quintupla (0, A, 1, B, -) indica che se la macchina si trova nello stato interno 0 e legge sul nastro il simbolo A, allora passa nello stato interno 1, scrive B sul nastro e non sposta la testina di lettura. 

La quintupla (1, B, 0, A, >) indica invece che se la macchina si trova nello stato interno 1 e legge sul nastro il simbolo B, allora passa nello stato interno 0, scrive A sul nastro e si sposta di una posizione a destra. Se ci si vuole spostare senza modificare il contenuto del nastro si può scrivere il simbolo appena letto utilizzando una quintupla analoga alla seguente: (1, B, 0, B, >).

Si noti che la scrittura del simbolo speciale "-" corrisponde a cancellare il contenuto di una cella. Ad esempio la quintupla (1, A, 2, -, -) indica che se la macchina si trova nello stato 1 e legge il simbolo A, allora passa nello stato 2 e cancella il simbolo A dal nastro non spostando la testina di lettura. Il simbolo "-" viene quindi utilizzato sia per rappresentare la cella vuota che per denotare il mancato movimento della testina. 

Si noti che una MdT può compiere un'azione anche quando incontra la cella vuota. Ad esempio la quintupla (2, -, 2, -, <) indica che se la macchina si trova nello stato 2 e legge una cella vuota allora lascia invariato il contenuto della cella e si sposta di una posizione a sinistra rimanendo nello stesso stato. 

Si noti infine che un insieme di quintuple associa ad ogni coppia: 

stato-interno-corrente, simbolo-letto

al più una tripla: 

prossimo-stato-interno, simbolo-scritto, direzione. 

Vediamo adesso come una MdT effettua i suoi calcoli. Inizialmente il nastro contiene una sequenza finita di simboli, detta sequenza di ingresso. La MdT è nel suo stato interno iniziale 0 con la testina posizionata sul simbolo più a sinistra nel nastro. A partire da questa configurazione iniziale, la MdT effettua una serie di azioni seguendo rigorosamente il suo insieme di regole. Se la macchina raggiunge uno stato interno per cui non esiste nessuna quintupla per la coppia: 

stato-interno-corrente, simbolo-letto

allora la MdT si ferma e termina la sua computazione. 

ESEMPIO 1. Consideriamo ad esempio una MdT che modifica una sequenza di A rimpiazzando ogni A in posizione dispari con una B (la prima A ha posizione pari uguale a 0). Una tale MdT può essere definita dal seguente insieme di regole: 

 

0	A	1	A	>
1	A	0	B	>
0	-	FINE	-	-
1	-	FINE	-	-

La prima quintupla stabilisce l'azione che la macchina deve eseguire quando si trova nello stato interno 0 e il simbolo in lettura è A. Tale situazione corrisponde ad una A in posizione pari Ad esempio consideriamo la situazione iniziale in cui la sequenza di ingresso è AA: 

La macchina si trova nello stato interno iniziale 0 ed il simbolo in lettura è A. (Graficamente rappresentiamo questa situazione indicando lo stato interno della macchina sopra la cella in lettura.) 

La prima quintupla stabilisce che la macchina deve cambiare il proprio stato interno in 1, scrivere il simbolo A sul nastro e spostarsi di una casella verso destra. Tale situazione corrisponde ad una A in posizione dispari, ottenendo: 

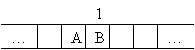
Dopo aver effettuato la prima mossa, la macchina si trova nello stato 1 ed in simbolo in lettura è B. In questo caso la seconda regola stabilisce che la macchina torna nello stato 0, scrivendo il simbolo A spostando la testina a destra di una cella, ottenendo così la nuova configurazione: 

Secondo quanto stabilito dalla terza regola, la macchina trova la casella bianca e si muove nello stato etichettato come FINE: 

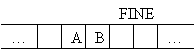
A questo punto la macchina si trova nello stato FINE e la cella in lettura è vuota. La macchina quindi si ferma, terminando la sua computazione, dato che non ha nessuna quadrupla che associ un'azione alla coppia (FINE, -). 

La macchina di esempio quindi una sequenza di simboli A in una sequenza in cui tutte le A in posizione dispari sono sostituite con una B. 

ESEMPIO 2. Si noti che una MdT può non terminare la sua computazione su certe sequenze di ingresso. Ad esempio la MdT definita dalle quintuple: 

 

0	A	1	A	>
1	A	0	A	<

non si fermerà mai per qualunque sequenza di ingresso che inizi per AA, perché continuerà a spostare la testina tra il primo e il secondo carattere dell'input. 

ESEMPIO 3. Dato un numero intero positivo n, n div 2 è il quoziente della divisione di n per 2. Ad esempio, 6 div 2 = 3 , mentre 9 div 2 = 4 . 

Consideriamo il problema di programmare una macchina di Turing che, dato un nastro iniziale contenente una sequenza composta da nA consecutive (con n > 1), termina la sua esecuzione lasciando sul nastro la sequenza composta da n div 2 A consecutive.

Ad esempio: 

 

nastro iniziale	nastro finale
AAAA	AA
AAAAA	AA
AAA	A
AA	A

Una MdT che risolva il problema in esame può ad esempio adottare la seguente strategia: 

1.    scorre la sequenza di ingresso, partendo dalla A più a sinistra;

2a.  se la sequenza di ingresso contiene una sola A, la cancella e si ferma;

2b.  se invece la sequenza di ingresso contiene almeno due A, le cancella entrambe e va ad aggiungere una A alla sequenza "di uscita", nella parte del nastro che si trova a destra della sequenza di ingresso. Quindi torna sulla cella più a sinistra di ciò che rimane della sequenza di ingresso e riparte da (1).

Una MdT che si comporti nel modo appena descritto può essere definita dal seguente insieme di quintuple: 

 

0	A	1	-	>
1	A	2	-	>
2	A	2	A	>
2	-	3	-	>
3	-	4	A	<
3	A	3	A	>
4	A	4	A	<
4	-	5	-	<
5	A	5	A	<
5	-	0	-	>
0	-	F	-	-

Lo stato 0 è utilizzato dalla macchina per cancellare la prima A dalla sequenza di ingresso, mentre lo stato 1 permette di cancellare la seconda A della sequenza, se esiste. Si noti che se la sequenza contiene soltanto una A allora la macchina si ferma nello stato 1 sulla cella vuota. Lo stato 2 permette di scorrere la parte rimanente della sequenza di ingresso, ovvero fino a quando non si incontra la cella vuota. A questo punto la macchina utilizza lo stato 3 per andare a scrivere una A a destra della sequenza "di uscita". Lo stato 4 serve quindi per ripercorre verso sinistra la sequenza di uscita, e lo stato 5 permette di controllare se la sequenza di ingresso contiene ancora qualche A. Se così è allora la macchina riporta la testina sul simbolo più a sinistra della sequenza di ingresso (stato 8) e riparte dallo stato 0, altrimenti la macchina si ferma nello stato F. 

Ad esempio per la sequenza di ingresso AAAA la MdT appena descritta esegue la seguente computazione: 

La macchina si ferma quindi nello stato F. 

Simulatore di macchine di Turing

I partecipanti alla gara di informatica per studenti delle scuole superiori utilizzano un simulatore di macchine di Turing di facile utilizzo anche per chi non ha dimestichezza con l'uso dei calcolatori. 

Il simulatore è stato scritto in Java e realizzato all'interno del Dipartimento di Informatica dell'Università di Pisa.

Molto brevemente, questo simulatore mostra sullo schermo una macchina di Turing (raffigurata come una specie di macchina a vapore) che corre su un nastro. Per esigenze di visualizzazione, lo spostamento della testina in una direzione è mostrato tramite lo spostamento del nastro nella direzione opposta, così da avere la testina sempre al centro dello schermo. Il simulatore inoltre mostra:

·        due ?finestre? in cui possono essere inserite direttamente le regole della macchina di Turing in corso di realizzazione (finestra verticale a destra) e il contenuto iniziale del nastro (finestra orizzontale in basso);

·        un pulsante CARICA per caricare le regole di una MdT da una lista di macchine date, ed un pulsante SALVA per memorizzare le modifiche apportate alle regole che definiscono la MdT;

·        i pulsanti ESEGUI e STOP per mettere al lavoro la macchina; il cursore sulla sinistra di ESEGUI permette inoltre di variare la velocità di esecuzione; la quintupla correntemente eseguita viene evidenziata di volta in volta nella finestra verticale a destra.

Una novità per rendere i programmi meno lunghi, consiste nel poter usare la seguente abbreviazione sintattica

( stato1, ABCD, stato2, EFGH, > )

per poter rappresentare concisamente la sequenza di tuple

( stato1, A, stato2, E, > )

( stato1, B, stato2, F, > )

( stato1, C, stato2, G, > )

( stato1, D, stato2, H, > ).

In generale, è possibile mettere n simboli dopo stato1 e dopo stato2, dove l?i-esimo simbolo dopo stato1 corrisponde all?i-esimo simbolo dopo stato2. Si noti che il numero di simboli dopo stato1 e stato2 deve corrispondere! Per esempio, è possibile descrivere le quintuple per scandire a destra una sequenza di A, B, C e D fino alla fine con due sole quintuple:

( 0, ABCD, 0, ABCD, > )

( 0, -, 1, -, < )

Un altro esempio consiste nel trasformare le A in B e le B in A in una sequenza contenente questi due soli simboli:

(0, AB, 0, BA, >)

Infine, per cancellare dal nastro una sequenza di simboli (per es., A, B, C, D), sostituendoli con uno spazio:

(0, ABCD, 0, - - - -, >).

Il simulatore sarà utilizzato durante la gara di informatica. Una versione semplificata di questo simulatore è accessibile all'indirizzo http://www.di.unipi.it/SettimanaCultura.