Esercizi di Gara della I edizione
-
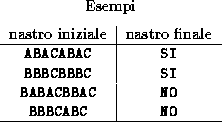
Programmare una Macchina di Turing che, dato un nastro iniziale contenente
la rappresentazione decimale di un numero intero positivo n (diverso
da 0), termina la sua esecuzione lasciando sul nastro la rappresentazione
decimale di n.

-
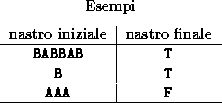
Programmare una Macchina di Turing che, dato un nastro iniziale contenente
una sequenza di
 e
e 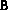 , termina la sua esecuzione lasciando sul nastro una sola
, termina la sua esecuzione lasciando sul nastro una sola  se la sequenza iniziale contiene almeno una
se la sequenza iniziale contiene almeno una 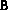 , una sola
, una sola 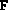 altrimenti.
altrimenti.
-
Programmare una Macchina di Turing che, dato un nastro iniziale contenente
una sequenza di cifre decimali, termina la sua esecuzione lasciando sul
nastro la sequenza che si ottiene eliminando tutte le cifre 0 alla sinistra
della cifra diversa da 0 più a sinistra. Se la sequenza iniziale
è composta da sole cifre 0, la macchina deve lasciare sul nastro
un solo 0.

-
Una sequenza si dice palindroma se la sua lettura da sinistra verso
destra è uguale alla sua lettura da destra verso sinistra. Programmare
una Macchina di Turing che, dato un nastro iniziale contenente una sequenza
di
 e
e 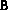 , termina la sua esecuzione lasciando sul nastro la sola sequenza
, termina la sua esecuzione lasciando sul nastro la sola sequenza 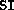 se la sequenza iniziale è palindroma, la sola sequenza
se la sequenza iniziale è palindroma, la sola sequenza 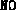 altrimenti.
altrimenti.

-
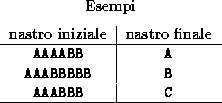
Indichiamo con
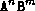 una sequenza del tipo
una sequenza del tipo
Programmare una Macchina di Turing che, dato un nastro iniziale
contenente una sequenza del tipo 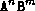 , con n > 0 e m > 0, termina la sua esecuzione lasciando
sul nastro una sola
, con n > 0 e m > 0, termina la sua esecuzione lasciando
sul nastro una sola  se n>m, una sola
se n>m, una sola 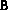 se m>n, una sola
se m>n, una sola 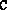 se n=m.
se n=m.
-
Indichiamo con
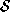 e
e 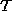 due generiche sequenze formate da
due generiche sequenze formate da  e
e 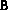 . Programmare una Macchina di Turing che, dato un nastro iniziale contenente
una sequenza del tipo
. Programmare una Macchina di Turing che, dato un nastro iniziale contenente
una sequenza del tipo 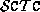 , termina la sua esecuzione lasciando sul nastro la sequenza
, termina la sua esecuzione lasciando sul nastro la sequenza 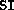 se
se 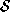 e
e 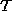 sono uguali, la sequenza
sono uguali, la sequenza  altrimenti.
altrimenti.
-
Programmare una Macchina di Turing che, dato un nastro iniziale contenente
una sequenza di
 e
e  , con almeno una
, con almeno una  , termina la sua esecuzione lasciando sul nastro la sequenza di sole
, termina la sua esecuzione lasciando sul nastro la sequenza di sole 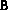 consecutive (cioè non separate da alcuno spazio) che si ottiene
da quella iniziale eliminando tutte le
consecutive (cioè non separate da alcuno spazio) che si ottiene
da quella iniziale eliminando tutte le  .
.
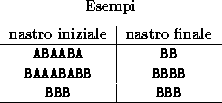
-
Dato un numero intero positivo n,
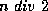 è il numero se n è pari, se n è dispari.
Ad esempio,
è il numero se n è pari, se n è dispari.
Ad esempio, 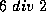 è il numero 3, mentre
è il numero 3, mentre 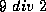 è il numero 4. Programmare una Macchina di Turing che, dato un nastro
iniziale contenente una sequenza composta da n
è il numero 4. Programmare una Macchina di Turing che, dato un nastro
iniziale contenente una sequenza composta da n  consecutive (con n > 1), termina la sua esecuzione lasciando sul
nastro la sequenza composta da
consecutive (con n > 1), termina la sua esecuzione lasciando sul
nastro la sequenza composta da 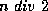
 consecutive.
consecutive.
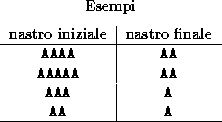
-
Programmare una Macchina di Turing che, dato un nastro iniziale contenente
una sequenza di
 e
e 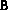 , termina la sua esecuzione lasciando sul nastro la sequenza che si ottiene
da quella iniziale rimpiazzando due o più
, termina la sua esecuzione lasciando sul nastro la sequenza che si ottiene
da quella iniziale rimpiazzando due o più  consecutive con una sola
consecutive con una sola  e due o più
e due o più 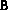 consecutive con una sola
consecutive con una sola 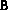 .
.

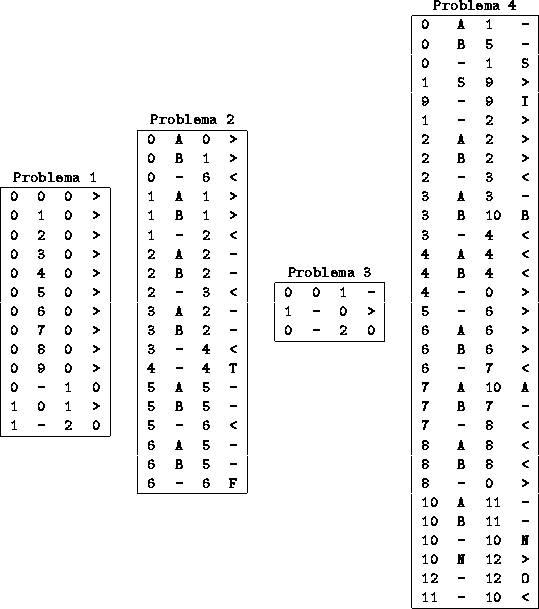
Soluzioni
Le soluzioni di seguito riportate sono quelle fornite dalla squadra
vincitrice della prima edizione della gara, ovvero da F. Benigni e V. Spina,
Liceo Scientifico Statale Barsanti e Matteucci, Viareggio (LU)).
Le soluzioni sono per la vecchia versione del simulatore delle
macchine di Turing, funzionante con le quadruple; il codice a
quintuple per il nuovo simulatore può essere facilmente dedotto.
Tutte le macchine di Turing realizzate dalla squadra vincitrice furono
infatti giudicate corrette dalla Giuria della prima edizione della gara.
Si noti che la Giuria considera una soluzione di un problema corretta se
la macchina di Turing corrispondente si comporta correttamente su tutti
i nastri di ingresso utilizzati dalla stessa Giuria per provare la macchina.
Pertanto le soluzioni di seguito presentate devono essere intese solo come
esemplificative. Inoltre la compattezza della soluzione fornita (ovvero
il numero di regole utilizzate) non rientra tra i criteri di valutazione
della giuria.